Rectangle Definition
adminse
Apr 01, 2025 · 8 min read
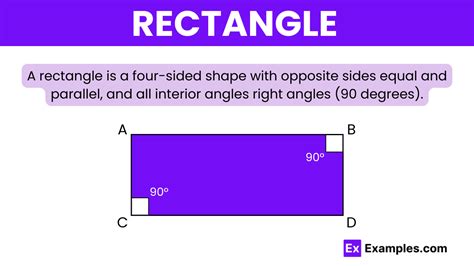
Table of Contents
Unveiling the Rectangle: More Than Meets the Eye
What makes the rectangle such a fundamental shape in mathematics and the real world?
The rectangle, a seemingly simple geometric figure, underpins countless aspects of our lives, from architecture and design to advanced mathematical concepts.
Editor’s Note: This comprehensive exploration of rectangle definitions and applications has been published today.
Why Rectangles Matter
The rectangle's importance transcends its simple appearance. It's a cornerstone of geometry, impacting fields ranging from construction and engineering to computer graphics and data visualization. Understanding its properties is crucial for numerous disciplines. Its prevalence in everyday objects – screens, buildings, furniture – makes understanding its characteristics essential for both practical applications and theoretical comprehension. The rectangle's properties also form the foundation for understanding more complex shapes and geometrical principles. For instance, the square, a special case of a rectangle, inherits all rectangular properties but adds the constraint of equal sides. This demonstrates the hierarchical nature of geometric shapes and how fundamental definitions build upon each other. Furthermore, the rectangle's properties play a crucial role in calculus, particularly in integration and optimization problems.
Overview of the Article
This article delves into the multifaceted world of the rectangle. We will explore its formal definition, key properties, different types, practical applications across various industries, and its significance in more advanced mathematical concepts. Readers will gain a deeper understanding of the rectangle's role in shaping our world and its importance in numerous fields.
Research and Effort Behind the Insights
This article draws upon established geometric principles, widely accepted mathematical definitions, and real-world examples from various disciplines. The information presented is based on rigorous mathematical definitions and extensive research into the practical applications of rectangles across numerous fields.
Key Takeaways
| Key Aspect | Description |
|---|---|
| Formal Definition | A quadrilateral with four right angles. |
| Key Properties | Opposite sides are parallel and equal in length; diagonals bisect each other. |
| Types of Rectangles | Square (all sides equal), Oblong (adjacent sides unequal) |
| Applications | Construction, design, computer graphics, data visualization, packaging, tiling, etc. |
| Mathematical Significance | Foundation for advanced concepts in geometry, calculus, and linear algebra. |
Smooth Transition to Core Discussion
Let’s now delve into the core aspects of the rectangle, beginning with its formal definition and progressing to its multifaceted applications and mathematical significance.
Exploring the Key Aspects of the Rectangle
-
The Formal Definition of a Rectangle: A rectangle is defined as a quadrilateral (a four-sided polygon) with four right angles (90-degree angles). This simple yet powerful definition forms the basis for all other properties and applications.
-
Properties of a Rectangle: Several key properties stem directly from the definition:
- Opposite sides are parallel: This means that opposite sides lie on parallel lines.
- Opposite sides are congruent (equal in length): This property ensures symmetry.
- All angles are right angles (90 degrees): This is the defining characteristic.
- Diagonals bisect each other: The diagonals intersect at their midpoints.
- Diagonals are congruent (equal in length): In a rectangle, the two diagonals are always equal in length.
-
Special Cases: The Square: A square is a special type of rectangle where all four sides are equal in length. It inherits all the properties of a rectangle but adds the additional constraint of equilateral sides.
-
Rectangles in Different Coordinate Systems: The definition and properties of a rectangle remain consistent regardless of the coordinate system used (Cartesian, polar, etc.). However, the representation and calculations might vary depending on the chosen system.
-
Applications of Rectangles: Rectangles are ubiquitous in the real world. Their inherent stability and ease of construction make them ideal for:
- Architecture and Construction: Buildings, rooms, windows, doors, and many structural elements are rectangular.
- Design: From furniture to artwork, rectangles are frequently employed for their aesthetic appeal and practical functionality.
- Packaging: Boxes, containers, and many packaged goods utilize rectangular shapes for efficient stacking and shipping.
- Computer Graphics and Image Processing: Pixels on a screen are arranged in a rectangular grid. Images are often manipulated using rectangular regions of interest.
- Data Visualization: Graphs, charts, and tables often utilize rectangular grids to organize and present data.
- Tiling and Tessellations: Rectangles are easily used to create repeating patterns in floor tiles, mosaics, and other applications.
Closing Insights
The rectangle, a seemingly simple shape, plays a crucial role in various aspects of mathematics, design, and engineering. Its inherent properties, including parallel and equal opposite sides and right angles, make it an ideal choice for construction, design, and many other applications. Understanding the rectangle’s definition and properties is fundamental to numerous fields, emphasizing its significance beyond its apparent simplicity. Its straightforward nature facilitates both practical applications and the building blocks for more complex geometrical concepts. The rectangle's pervasiveness underscores its fundamental importance in our understanding and interaction with the world around us.
Exploring the Connection Between Area and Rectangles
The area of a rectangle, a fundamental concept in geometry, directly relates to its dimensions. The area is calculated by multiplying the length and width: Area = length × width. This simple formula has far-reaching implications. In construction, for instance, accurate area calculations are crucial for material estimation and cost analysis. In design, understanding the area allows for optimizing space usage and maximizing functionality. In computer graphics, pixel area calculations are fundamental to image rendering and manipulation. The concept of area, therefore, is inextricably linked to the rectangle and its practical applications. Errors in area calculation can have significant consequences, leading to inaccuracies in material estimation, design flaws, or incorrect image rendering.
Further Analysis of Area
The concept of area extends beyond simple rectangles. More complex shapes often require breaking them down into smaller rectangles or utilizing integration techniques to calculate their area accurately. However, the rectangular area calculation serves as a foundational building block for these more advanced methods. Understanding area's dependence on length and width allows for optimizing designs for maximum area within given constraints, a common problem in various engineering and architectural applications.
| Shape | Area Calculation | Application Example |
|---|---|---|
| Rectangle | Length × Width | Calculating the floor space of a room |
| Square | Side × Side | Determining the size of a square plot of land |
| Irregular Shape | Decomposition into rectangles + integration | Estimating the area of an irregularly shaped field |
FAQ Section
-
Q: What is the difference between a rectangle and a square? A: A square is a special type of rectangle where all four sides are equal in length. All squares are rectangles, but not all rectangles are squares.
-
Q: What are the diagonals of a rectangle? A: The diagonals are line segments connecting opposite corners of the rectangle. They bisect each other (intersect at their midpoints) and are equal in length.
-
Q: How is the perimeter of a rectangle calculated? A: The perimeter is the total distance around the rectangle. It is calculated as 2 × (length + width).
-
Q: What are some real-world examples of rectangles? A: Buildings, doors, windows, books, computer screens, television screens, and many more everyday objects.
-
Q: How is a rectangle used in computer graphics? A: Rectangles define the boundaries of images, shapes, and text on a screen. They are fundamental to image manipulation and rendering.
-
Q: Can a rectangle have only three right angles? A: No. If three angles are right angles (90 degrees), the fourth angle must also be a right angle to ensure the sum of angles in a quadrilateral is 360 degrees.
Practical Tips
-
Accurate Measurement: When working with rectangles, ensure accurate measurements of length and width to avoid errors in area and perimeter calculations.
-
Understanding Scale: In architectural or engineering drawings, pay close attention to the scale to accurately translate dimensions from the drawing to the real world.
-
Utilizing Grid Systems: Employing grid systems simplifies the design and construction of rectangular structures, ensuring accurate alignment and proportions.
-
Optimizing Area: In design, strive to maximize the usable area within a given rectangular space to enhance functionality and efficiency.
-
Using Software Tools: Utilize CAD (Computer-Aided Design) or other software tools for precise calculations and visualizations when working with rectangular shapes.
-
Applying Geometric Theorems: Leverage geometric theorems (such as the Pythagorean theorem for calculating diagonal lengths) to solve problems related to rectangles.
-
Considering Aspect Ratio: The aspect ratio (ratio of length to width) influences the overall appearance and functionality of a rectangle. Consider the appropriate aspect ratio based on the specific application.
-
Efficient Packing: In packaging and logistics, understanding rectangular shapes helps optimize packing strategies to minimize wasted space and improve efficiency.
Final Conclusion
The rectangle, despite its seemingly simple definition, holds immense significance in both theoretical mathematics and practical applications. From the foundational principles of geometry to the design of buildings and the rendering of images, the rectangle's properties and applications are widespread. This comprehensive exploration has highlighted the rectangle's importance across diverse fields, showcasing its enduring relevance in shaping our world. Further investigation into its properties and applications can unlock even deeper insights into its role in numerous disciplines. Understanding the rectangle is more than just recognizing a shape; it is understanding a fundamental building block of our physical and mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about Rectangle Definition . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.